Künstliche-Intelligenz: Billard Roboter
Auf dieser Seite findest du die Dokumentation zum Software Praktikum "Billard Roboter - Künstliche-Intelligenz-Modul (KI)". Im SS2004 habe ich zusammen mit einem Kommilitonen an diesem Projekt gearbeitet und eine Künstliche Intelligenz für einen Billard-spielenden Roboter entwickelt, der in den Robotik-Räumen der FH-Wedel aufgebaut war.
![]() Download des Programms 'Künstliche Intelligenz für Billard Roboter' (Win32 Executable)
Download des Programms 'Künstliche Intelligenz für Billard Roboter' (Win32 Executable)
1. Inhaltsverzeichnis
3.1 Programmierumgebung und Kompilierung
3.2 Skizze des Billard-Tisches:
3.3 Allgemeine physikalische Billard-Grundlagen
3.3.1 Kollision zwischen Kugeln
3.4 Berechnung des nächsten Stoßes:
3.4.3 Weiße → Bande → Kugel → Loch
3.4.4 Weiße → Kugel → Bande → Loch
3.4.5 Weiße → Kugel → Kugel → Loch
3.4.6 Versuchen Kugel anzuspielen (kein Foul)
3.5 Physikalische Formel zur Anstoßgeschwindigkeitsberechnung
3.6 Prüfung, ob eine Kugel im Weg liegt
3.7 Prüfung, ob die Bande im Weg einer berechneten Bahn liegt:
3.8 Berechnung des Anspielpunktes einer Bande für den "Weiße→Bande→Kugel" - Stoß:
3.8.1 Empfang und Auswertung eines KI-Requests
3.8.2 Konstruktion und Senden des KI-Result-Dokuments
3.8.3 Konstruktion und Senden des KI-Status-Dokuments
2. Benutzerhandbuch
2.1 Programminstallation
Um das Programm fehlerfrei ausführen zu können,
müssen die Dateien "ki-status.xml", "ki-result.xml" und "config.ini" im selben Verzeichnis liegen, wie das Hauptprogramm "billardki.exe".
2.2 Bedienungsanleitung
2.2.1 Aufbau der Ini-Datei
Die Konfigurationseinstellungen sind in der INI-Datei "config.ini" abgespeichert, die in dem selben Verzeichnis wie die EXE-Datei zu finden ist. Diese Datei ist in folgende Sektionen aufgeteilt:
- tisch
- toleranz
- kugeln
- physik
- netzwerk
Da die meisten Werte aus der INI-Datei intern als Zahlen mit Nachkommastellen verwendet werden, sind die meisten Werte in der INI-Datei mut 100 multipliziert, wodurch das Komma entfällt.
2.2.1.1 Sektion 'tisch'
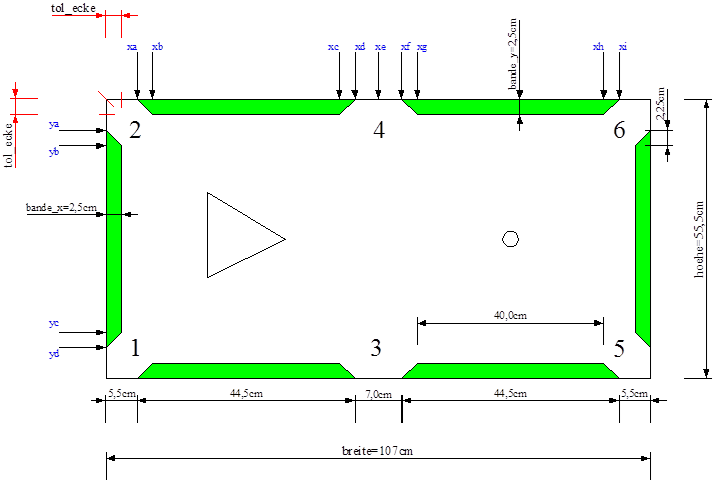
In dieser Sektion werden alle Parameter definiert, die den Billardtisch beschreiben:
- breite, hoehedie Breite und Höhe des Tisches (cm/100)
- bande_x, bande_ydie Dicke der horizontalen und der vertikalen Bande (cm/100)
- xa-xi, ya-yidie Parameter für die Spezifikation der Größe der Banden und der Löcher.
Siehe dazu auch die Skizze in 3.2. Der Bezugspunkt für alle Parameter ist oben links.
2.2.1.2 Sektion 'toleranz'
In dieser Sektion werden die Toleranzen für die Algorithmen der KI definiert
- tol_eckeAbstandder drei Punkte eines Loches
- tol_abstandAbstand von Bande, zu anderen Kugeln etc.
- tol_winkelMindestwinkel bei der Stoßberechnung
2.2.1.3 Sektion 'kugeln'
In dieser Sektion werden die Parameter für jede einzelne Kugel definiert
- durchmesserDurchmesser aller Kugeln
- k[num]_xX-Position der Kugel auf dem Tisch (cm/100) (Ursprung unten links)
- k[num]_yY-Position der Kugel auf dem Tisch (cm/100) (Ursprung unten links)
- k[num]_inlochgibt an, ob sich die Kugel im Loch befindet (Positionen dann nicht relevant)
- k[num]_zieltaschegibt die Zieltasche an, in der die Kugel gespielt werden soll
[num] ist hier ein Platzhalter für die Zahlen 0 – 16. (0 = weiße Kugel, 1-15 = Spielkugeln)
2.2.1.4 Sektion 'physik'
In dieser Sektion werden die physikalischen Konstanten definiert, die für die Geschwindigkeitsberechnung der Kugeln auf dem Tisch relevant sind
- uReibungskoeffizient des Filzbelags (1/100)
- gErdbeschleunigung (m/s/100)
- kElastizitätskonstante der Bande (1/100)
- vmaxmaximale Anfangsgeschwindigkeit der weißen Kugel (m/s/100)
- vendEndgeschwindigkeit, mit der die Spielkugel ins Loch fällt
2.2.1.5 Sektion 'netzwerk'
In dieser Sektion werden die Einstellungen für die Netzwerkanbindung vorgenommen
- portDer Port, auf dem unser KI-Modul die Requests erwartet
- bportDer UDP-Port, an den ein Broardcast mit der aktuellen Statusmeldung versendet wird
2.2.2 Die Programmoberfläche
Nach erfolgreichem Programmstart erscheint die Programmoberfläche zur Steuerung und Visualisierung des KI-Moduls:
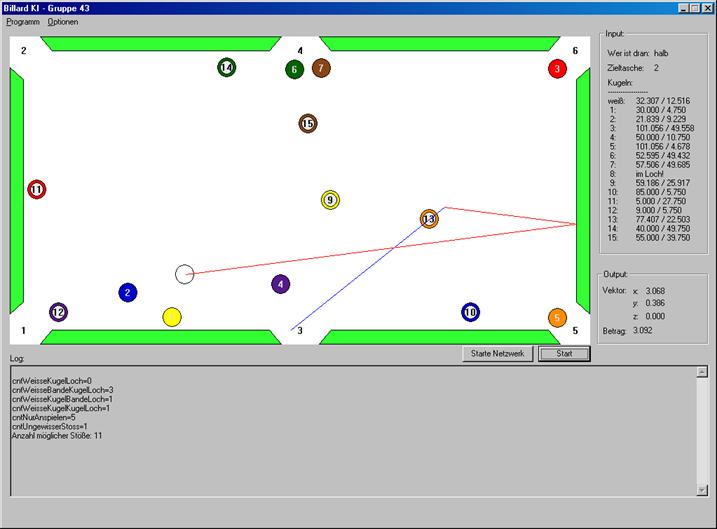
Man sieht hier den Billardtisch mit den aktuellen Positionen der Kugeln.
Jede der Kugeln ist per Drag and Drop auf dem Tisch frei verschiebbar, somit kann jede Spielsituation simuliert werden. Per Klick auf den Button „Start“ werden sämtliche möglichen Stöße berechnet und der leichteste Stoß angezeigt. Im Menü „Optionen“ kann noch definiert werden, welche Kugeln gerade aktiv sind (halbe, volle, alle Kugeln). Rechts vom Tisch sind die Informationen über die Input- und Outputdaten zu entnehmen.
Im Logfenster werden Statusmeldungen über den aktuell durchgeführten Stoß angezeigt.
Durch Klick auf den Button „Starte Netzwerk“ wird der Netzwerkserver eingeschaltet. Wird ein KI_Request (in Form einer XML-Datei) empfangen, wird aus den empfangenen Inputwerten der bestmögliche Stoß berechnet, welcher an den im Request spezifizierten Socket (in XML-Form) gesendet wird. Der durchgeführte Stoß wird außerdem auf dem Billardtisch dargestellt. Bei jedem An- und Ausschalten des Netzwerkservers wird außerdem eine Statusmeldung per UDP-Broardcast versandt.
3. Programmierhandbuch
3.1 Programmierumgebung und Kompilierung
3.1.1 Programmierumgebung
Für dieses Projekt wurde die Microsoft Visual C++ 6.0 Programmierumgebung genutzt. Das Programm startet als klassische Windows-Anwendung und benutzt keine Klassenbibliotheken (wie z.B. die MFC) als grafische Kapselung. Auf die entsprechenden Bibliotheken kann deshalb bei der Kompilierung verzichtet werden.
3.1.2 Compilereinstellung
Das Kompilieren sollte bereits mit den Standardeinstellungen von Visual C++ und den eingestellten Projektoptionen möglich sein. Auf spezielle Tools und Pfadeinstellungen wurde verzichtet.
An den Projekteinstellungen wurden folgende Änderungen durchgeführt (die in den Projekteinstellungen abgespeichert wurden und im Fehlerfalle korrigiert werden können):
- In der Kategorie „Code Generation“ ist die Laufzeitbibliothek auf „Multithreaded“ gestellt (der TCP-Server läuft in einem eigenem Thread ab)
- Zu Optimierungszwecken wurde die „Struct-Element-Ausrichtung“ auf 4 Bytes runtergesetzt
- Auf vorcompilierte Header wurde verzichtet
- Neben den standardmäßig eingebundenen Objekt-/Bibliothek-Modulen des Linkes wird die Library für die Windows Sockets 2 eingebunden. Dies geschieht in der Datei „netzwerk.cpp“ durch den Aufruf der Compileranweisung: „#pragma comment (lib, "ws2_32.lib")“
Alle wichtigen Parameter der Anwendung werden beim Programmstart aus der INI-Datei „config.ini“ gelesen. Damit diese gefunden wird, sollte sie sich im gleichen Verzeichnis wie die Exe-Datei befinden (Release-Ordner)
3.2 Skizze des Billard-Tisches:
Die untenstehende Zeichnung zeigt den Aufbau und die Abmessungen des Billardtisches, der für das Spiel und den Roboter eingesetzt wird. Die Werte xa – xi und ya – yd stehen dabei als Beschreibung für die Strecken von der linken oberen Ecke bis zum eingetragenen Punkt. Der Tisch ist symmetrisch, so dass die Abstände an den gegenüberliegenden Seiten den selben Verhältnissen entsprechen:
3.3 Allgemeine physikalische Billard-Grundlagen
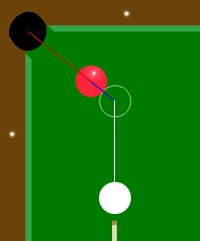
3.3.1 Kollision zwischen Kugeln
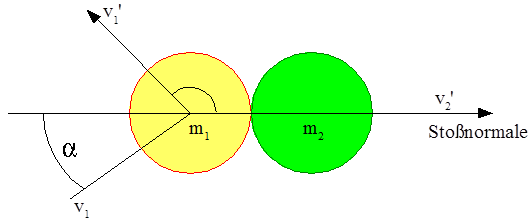
Die Abbildung zeigt einen typischen, direkten Billard-Stoß. Nach der Kollision der Kugeln wird die rote Kugel in die Richtung gestoßen, die der Verbindung der beiden Kugelmittelpunkte entspricht (blaue Linie). Die weiße Kugel wird entsprechend dem Winkel zur angestoßenen farbigen Kugel, abgelenkt. Nach dem Zusammentreffen wird die rote Kugel auf das Loch zurollen, die Weiße hingegen wird nach rechts zurücklenkt.
3.3.2 Banden
Die Kugel prallt in etwa im gleichen Winkel von der Bande ab, in welchem sie darauf zugerollt ist (Einfallswinkel = Austrittswinkel).
Das Abprallen nach einem senkrechten Auftreffen hängt vom Effet der Kugel ab.
Bei entsprechender Ausrichtung des Queues kann sich die Kugel durch Effet in einer Kurve bewegen. Effet-Stöße werden bei dem aktuellen Projektstand jedoch nicht unterstützt.
3.4 Berechnung des nächsten Stoßes:
3.4.1 Einleitung
Die Künstliche Intelligenz wird bei der Berechnung versuchen, den nächsten Stoß so zu ermitteln, dass er vom Billard-Roboter möglichst einfach durchzuführen ist. Dafür wird ein Punktesystem benutzt, das jeden berechneten Stoß eine „Durchführungsschwierigkeit“ zuweist. Je geringer dieser Wert ist, desto einfacher wird der Stoß eingestuft und desto wahrscheinlicher wird eine erfolgreiche Umsetzung des Roboters werden. Die Künstliche Intelligenz kennt dabei die folgenden unterschiedlichen Spielzüge, die im wesentlichen absteigend betrachtet immer schwieriger und komplizierter werden:
- Weiße → Kugel → Loch
- Weiße → Bande → Kugel → Loch
- Weiße → Kugel → Bande → Loch
- Weiße → Kugel → Kugel → Loch
- Eigene Kugel linear anspielen (ohne Versenken der Kugel)
- Ungewisser Stoß (keine Taktik, nur wenn alle Berechnungen versagen)
3.4.2 Weiße → Kugel → Loch
Dieses ist das einfachste Verfahren, eine Kugel zu versenken. Eine Kugel wird mit der weißen Kugel so direkt angespielt, dass sie ohne weitere Kollisionen in ein Loch rollt. Die linke Abbildung zeigt den genauen Bahnenverlauf der Kugeln. Um den Punkt zu berechnen, an dem die weiße Kugel die Farbige treffen soll (pAnspielpunkt), wird vom Loch aus rückwärts zurückgerechnet. Zunächst wird der Vektor vom Loch zur Kugel gebildet (v). Anschließend wird er um den Kugeldurchmesser (d) verlängert. Der neu entstandene Vektor zeigt somit genau vom Loch zum Anspielpunkt. Von diesem Anspielpunkt kann nun ein zweiter Vektor zur weißen Kugel gebildet werden (vAnspielpunkt). Der Verlauf der Bahnen ist somit definiert. In der Praxis ist außerdem der Anspielwinkel (α) entscheidend, da Stöße mit Anspielwinkeln in der Nähe von 90° sehr viel schwerer sind, als "gerade" Stöße!

Die Künstliche Intelligenz wendet dieses Verfahren auf alle Löcher und auf alle "eigenen" Kugeln an, um den optimalen Stoß zu ermitteln. Liegt eine andere Kugel im Anspiel-Weg des berechneten Stoßes oder ist ein Anspielwinkel zu dicht an 90° wird die aktuelle Berechnung als Ergebnis verworfen.
3.4.3 Weiße → Bande → Kugel → Loch
Bei diesem Spielzug wird eine Kugel nicht direkt mit der Weißen angespielt, sondern die Weiße trifft zunächst auf eine Bande und spielt erst nach dem Abprallen eine Spielkugel an (klassischer Bandenstoß). Diese Technik ist besonders interessant, wenn der direkte Weg zwischen Weißer und Spielkugel versperrt ist.
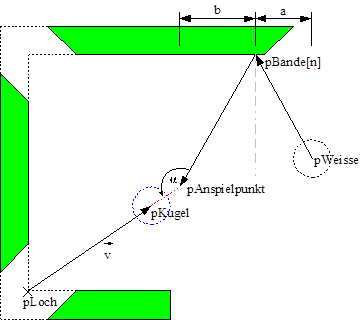
Die Berechnung der Spielbahn und der benötigten Punkte erfolgt bei diesem Spielzug wieder rückwärts. Vom Zielloch (pLoch) ausgegangen wird anfangs ein Vektor zur Kugel gebildet (v). Dieser wird anschließend um den Kugeldurchmesser verlängert, so dass der Vektor auf den Anspielpunkt (pAnspielpunkt) zeigt.
Als nächster Schritt muss der Bandentreffpunkt zwischen pAnspielpunkt und der weißen Kugel (pWeisse) ermittelt werden. Dies wird mit Hilfe des Strahlensatzes und der Verhältnisse der Längen a und b durchgeführt. Dabei gilt Eintrittswinkel = Austrittswinkel. Der genau mathematische Rechenweg wird in Kap. 3.8 erläutert! Ist der Bandenpunkt gefunden kann ein Vektor von der weißen Kugel zu dem Bandenpunkt gebildet werden.
Auch diese Rechenschritte werden von der Künstlichen Intelligenz iterativ auf alle Löcher, alle vier Banden (links, oben, rechts, unten) und alle „eigenen“ Kugeln durchgeführt, bis der beste Spielzug feststeht. Bei den „langen Banden“ kommt außerdem eine Einschränkung hinzu, da diese Banden aufgrund der Mittellöcher unterbrochen sind. Fällt der berechnete Bandenpunkt innerhalb des unterbrochenen Bereichs, wird der Stoß ungültig bzw. nicht ausführbar.
3.4.4 Weiße → Kugel → Bande → Loch
Dieses Verfahren dehnt die Anspielmöglichkeiten weiter aus und ermöglicht auch erfolgreiches Anspielen einer Kugel, wenn andere Kugeln im Weg liegen und die direkte lineare Anspielbahn versperrt ist (zwischen Kugel und Loch). Es wird versucht, mit der Weißen eine Kugel so anzuspielen, dass diese über eine Bande ins Loch läuft.
Die Berechnung dieses Spielzuges erfolgt in ähnlicher Weise wie im vorigen Abschnitt beschrieben. Allerdings ist die Reihenfolge vertauscht. Es wird auch hier vom Loch an rückwärts zum Anspielpunkt gerechnet. Zunächst wird der Treffpunkt an der Bande bestimmt (siehe auch Kap. 3.8). Davon ausgehend kann anschließend der Anspielpunkt für die Weiße Kugel ermittelt werden. Dazu wird der Vektor vom Bandentreffpunkt zur Kugel um den Kugeldurchmesser verlängert. Vom Anspielpunkt erstreckt sich dann ein Vektor zur weißen Kugel.
3.4.5 Weiße → Kugel → Kugel → Loch
Wenn die Künstliche Intelligenz keine direkten oder Bandenstöße berechnen kann, kommt dieses Verfahren zum Einsatz. Bei diesem Spielzug wird versucht mit der Weißen eine Kugel (Kugel2) anzuspielen, die dann eine weitere Kugel (Kugel1) anstößt, welche dann im Loch versenkt wird. Insbesondere wenn zwei Kugeln nahe beieinander und in der Nähe eines Loches liegen, ist dieser Spielzug sinnvoll.
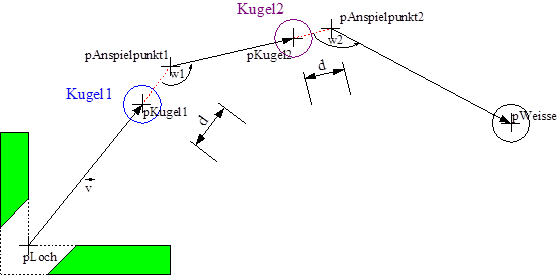
Die Berechnung wird auch bei diesem Spielzug von hinten angegangen. Es wird zunächst der Vektor (v) vom Zielloch zu Kugel1 bestimmt. Um dann den Anspielpunkt der Kugel (pAnspielpunkt1) zu finden, muss der Vektor (v) um den Kugeldurchmesser (d) verlängert werden.
Dieser Anspielpunkt (pAnspielpunkt1) entspricht jetzt dem neuen Ziel von Kugel2. Von dem Punkt ausgehend wird zur zweiten Kugel ein weiterer Vektor gebildet, der ebenfalls um den Kugeldurchmesser (d) verlängert wird. Dadurch zeigt er genau auf den Anspielpunkt der zweiten Kugel (pAnspielpunkt2). Dies ist der Zielpunkt für die weiße Kugel. Ein Vektor zur weißen Kugel (pWeisse) erzeugt die Spielbahn.
Wie bei den anderen Verfahren berechnet die Künstliche Intelligenz iterativ jede Möglichkeit für alle Paare der „eigenen“ Spielkugeln und alle Löcher, um den optimalen Stoß zu finden.
3.4.6 Versuchen Kugel anzuspielen (kein Foul)
Konnten alle vorigen Verfahren keinen möglichen Spielzug ermitteln, wird nun zumindest versucht, eine „eigene“ erlaubte Kugel anzuspielen. Das Ziel ist es hier, ein Foul durch unerlaubtes Anspielen zu verhindern. Es kann zwar keine eigene Kugel eingelocht werden, aber evtl. ist es möglich sie zumindest anzuspielen.
Diese Prüfung wird linear durchgeführt, ein Anspielen ist also nur möglich, wenn zwischen Weißer und mindestens einer „eigenen“ Kugel keine weitere Kugel im Weg liegt.
Eine Optimierung wäre, die eigene Kugel nur streifen zu lassen (nicht am Mittelpunkt anspielen) oder sogar Umwege über Banden zu berechnen. Dieses Verhalten ist im aktuellen Projektstand jedoch nicht implementiert.
3.4.7 Ungewisser Stoß
Das letzte Verfahren wird benutzt, wenn die Lage der Kugeln so verstrickt ist, dass selbst das Anspielen einer „eigenen“ Kugel nicht mehr möglich ist. Es wird ein Stoß vorgegeben, der mechanisch immer durchführbar ist jedoch nahezu keine Trefferchance aufweist und in vielen Fällen zu einem Foul führen wird. Um diesen Stoß nicht „zufällig“ zu ermitteln, wird die Bahn durch die Lage der weißen Kugel beeinflusst. Es wird von der weißen Kugel ausgehend auf die gespiegelte Position (x- und y-Achse) vom Mittelpunkt des Tisch geschlagen.
3.5 Physikalische Formel zur Anstoßgeschwindigkeitsberechnung
Die gewünschte Spielkugel wird mit einer definierten Endgeschwindigkeit in ein Loch fallen. Damit dies erfüllt werden kann, muss berechnet werden, wie groß die Anfangsgeschwindigkeit der weißen Kugel unmittelbar nach dem Stoß sein muss. Diese Anfangsgeschwindigkeit v0 kann quasi „rückwärts“ ausgerechnet werden.
Dies soll an dem folgenden Beispielstoß erläutert werden:
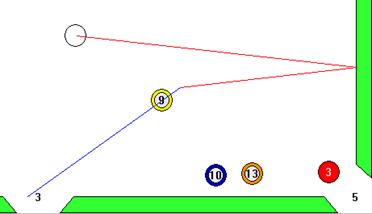
- Da die Bremsbeschleunigung durch die Reibung der Kugel auf dem Filzbelag bekannt ist, lässt sich die Geschwindigkeit vanf berechnen, welche die Spielkugel haben muss, damit sie mit der definierten Endgeschwindigkeit ins Loch fällt. Dies kann mithilfe folgender Formel berechnet werden:
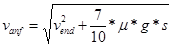
- Als nächstes muss die Auftreffgeschwindigkeit der weißen Kugel auf die Spielerkugel berechnet werden:
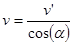
Durch diese Skizze wir der Sachverhalt deutlicher:
- Anschließend wird die Geschwindigkeit berechnet, die die Kugel nach dem Bandenaufprall hat, was ebenfalls mithilfe der Filzreibung und der zurückgelegten Strecke geschieht
- Da durch den Bandenaufprall Energie, und damit Geschwindigkeit verloren geht, muss dieses in der Berechnung berücksichtigt werden, was durch folgende Formel realisiert wird:
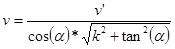
Durch diese Skizze wird der Sachverhalt deutlicher:

- Zum Schluss kann dann mit der Streckenformel die Anfangsgeschwindigkeit der weißen Kugel berechnet werden.
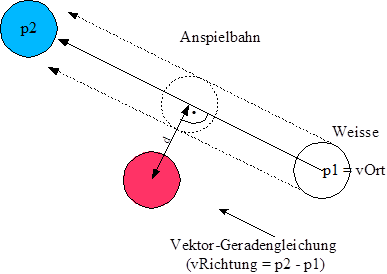
3.6 Prüfung, ob eine Kugel im Weg liegt
Eine wichtige und häufig genutzte Funktion ist die Prüfung, ob eine Kugel in einer Anspielbahn "im Weg" liegt:
|
|
Die linke Abbildung zeigt eine Anspielbahn von der weißen zur blauen Kugel. Um zu berechnen, ob eine Kugel dazwischen liegt, wird zunächst eine Vektor-Geradengleichung der Anspielbahn erzeugt. Diese besteht aus einem Ortsvektor (vOrt) und den eingezeichneten Richtungsvektor (vRichtung). Mit Hilfe des Punktprodukts aus der Vektoralgebra lässt sich nun der kürzeste Abstand (d) von einem beliebigen Punkt (hier den Mittelpunkt der roten Kugel) zur Geraden zwischen p1 und p2 (die Anspielbahn) bestimmen. Ist der Abstand (d) kleiner als der Durchmesser der roten Kugel, so liegt die rote Kugel in der Anspielbahn, andernfalls befindet sie sich außerhalb. |
3.7 Prüfung, ob die Bande im Weg einer berechneten Bahn liegt:
Bei Stößen die in der Nähe einer Bande verlaufen, kann es vorkommen, dass die Bahn durch die Bande hindurch verlaufen würde.
Die folgende Abbildung zeigt dafür ein Beispiel:

Um das Kollidieren mit der Bande bei der Berechnung abfangen zu können, bekommt jede Bande zwei Punkte zugeteilt (jeweils die Eckpunkte). Zu diesen Bandeneckpunkten wird dann mit Hilfe des Punktprodukts die kürzeste Entfernung zur Bahn berechnet (ähnlich wie bei der Prüfung, ob eine Kugel im Weg liegt). Ist die Entfernung kleiner als der Radius der Kugel, würde diese unterwegs an die Bande stoßen.
3.8 Berechnung des Anspielpunktes einer Bande für den „Weiße→Bande→Kugel“ - Stoß:
Bei Bandenstößen ist es besonders wichtig den richtigen Punkt an der Bande anzuspielen, damit die Kugel im richtigen Winkel zurückrollt. Für den Verlauf der Bahn gilt dabei das einfache Gesetz: Eintrittswinkel = Austrittswinkel. Die Berechnung des Punktes kann deswegen sehr gut mit Hilfe des Strahlensatzes erfolgen. Die untenstehende Abbildung zeigt den Weg, den die Kugel über die Bande nehmen soll. Zusätzlich sind alle wichtigen Hilfslinien für die Berechnung eingezeichnet. Die Künstliche Intelligenz sind zu Beginn die beiden Positionen der Kugeln (Weiße und Anspiel-Kugel) bekannt. Zwischen diesen beiden Punkten liegt der Anspielpunkt an der Bande, durch die beiden Teilstrecken a und b beschrieben. Es gilt also jeweils darum, die konkreten Werte für a und b zu berechnen:
Obere Bande:
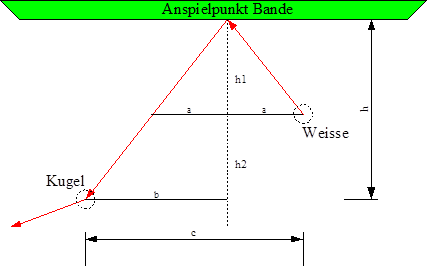
Berechnung des Banden-Anspielpunktes (a und b):
Der X-Wert des Bandenpunktes ergibt sich aus:
Weisse.x – a oder Kugel.x + b
Ansatz durch Strahlensatz:
![]()
für a gilt aber auch:
![]()
daraus ergibt sich:
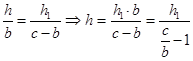
und schließlich die Formel zur Berechnung von b und somit des Bandenpunktes:
![]()
3.9 XML-Schnittstelle
3.8.1 Empfang und Auswertung eines KI-Requests
Die XML-Datei für den KI-Request wird als nullterminierter String empfangen. Dieser String wird nun nach folgendem Schema geparst: Mit der Funktion „getSubtag“ wird ein bestimmter Unterbereich des Dokuments zurückgegeben, der durch ein bestimmtes Anfangs- und Endetag definiert ist.
Von diesem Unterbereich kann dann ein weiterer Unterbereich extrahiert werden usw., bis ein Unterbereich genau den gesuchten Wert enthält, der dann in die Inputstruktur eingelesen werden kann.
Folgende Daten werden für jede Kugel ausgelesen:
- x-posititionX-Position der Kugel auf dem Tisch
- y-positionY-Position der Kugel auf dem Tisch
- bagcountgibt an, die wievielte versenkte Kugel diese Kugel ist. Für das Programm ist
nur relevant, ob sich die Kugel schon in einem Loch befindet oder nicht
- targetspezifiziert die Zieltasche, in welche die Kugel gespielt werden soll
Folgende Daten werden für den Status des Netzwerkverkehrs ausgelesen:
- ipv4Die IP-Adresse des Rechners, an den das Result-Dokument gesendet wird
- portDer Port, an dem jener Rechner lauscht
3.8.2 Konstruktion und Senden des KI-Result-Dokuments
Wenn das Ergebnis aus der Berechnung des Moduls versendet werden soll, muss dieses in das XML-Result-Dokument eingebunden werden. Dazu wird zunächst die Musterdatei („ki-result.xml“) als nullterminierten String eingelesen. Anschließend werden die zu sendenden Werte in diesen XML-String eingefügt:
- x-componentDie X-Komponente des Ergebnisvektors
- y-componentDie Y-Komponente des Ergebnisvektors
- runningDer Aktivitätsstatus dieses Moduls
- portDer Port, auf dem dieser Rechner auf TCP-Pakete lauscht
- ipv4Die IP-Adresse dieses Rechners
Der fertige XML-String kann anschließend uber das Netzwerk an den Socket geschickt werden, der im Request spezifiziert worden ist
3.8.3 Konstruktion und Senden des KI-Status-Dokuments
Bei dem Versenden des Status’ wird genau so verfahren, wie bei dem Versenden des Results. Es werden jedoch nur die "running", "port" und "ipv4" Werte versendet. Die Musterdatei ist hier "ki-status.xml".
Das Statusdokument wird per Broadcast via UDP versendet. Beim einschalten des Servers wird ein Dokument mit running = true, beim Ausschalten ein Dokument mit running = false gesendet. So ist Sichergestellt, das jeder relevante Rechner im Netzwerk weiß, ob das Modul aktiv ist oder nicht.
Kommentare 1
Wow this article Billiard is an exciting one. Technology now a day is really fast growning. Alright!
Neuen Kommentar schreiben: