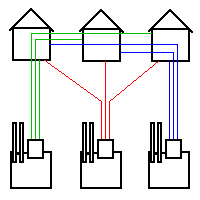
Rätsel: Häuser geschickt mit Strom versorgen
Update: Freitag, 27. September
Man hat 3 Wohnhäuser, die nebeneinander stehen.
Darunter sind 3 weitere Gebäude, nämlich:
- ein Kraftwerk,
- ein Wasserwerk und
- ein Gaswerk
Die Anordnung sieht also dementsprechend so aus:
Jedes Wohnhaus (H1, H2, H3) muss nun eine Verbindung zu diesen Werken (W1, W2, W3) haben. Also: Die Häuser und die Werke müssen JE DREI Anschlüsse haben.
Jetzt der Haken: Die Verbindungen dürfen sich NICHT überkreuzen und jedes Wohnhaus muss seine eigene Verbindung haben.
Wie gefällt dir dieses Rätsel mit den Häuserverbindungen? Hast du weitere Ideen oder Anmerkungen? Schreibe doch einen Kommentar...
Kommentare 20
Name (2013-10-12)
Wenn die Leitungen durch die Häuser gehen dürfen ist das ja voll einfach!
Wenn die Leitungen durch die Häuser gehen dürfen ist das ja voll einfach!
Fruko (2013-11-13)
Wo ist die Lösung?
Wo ist die Lösung?
entropie (2014-02-22)
das funktioniert nunmal nicht mit "punktförmigen" häusern. die angegebene lösung widerspricht sich übrigens mit der angabe: "..jedes Wohnhaus muss seine eigene Verbindung haben". das ist im rahmen des zugrundegelegten gestaltungsspielraumes weder logisch noch konsequent.
das funktioniert nunmal nicht mit "punktförmigen" häusern. die angegebene lösung widerspricht sich übrigens mit der angabe: "..jedes Wohnhaus muss seine eigene Verbindung haben". das ist im rahmen des zugrundegelegten gestaltungsspielraumes weder logisch noch konsequent.
hv (2014-03-24)
Ich kenne die Angabe weder kreuzen noch durch ein Haus,auch nicht 3D,DAS ist allerdings unmöglich,haben es getestet
Ich kenne die Angabe weder kreuzen noch durch ein Haus,auch nicht 3D,DAS ist allerdings unmöglich,haben es getestet
GenieBlue (2014-06-15)
Einfach. Wer sagt, dass die Verbindungen gerade sein müssen? XD
Einfach. Wer sagt, dass die Verbindungen gerade sein müssen? XD
Fritz (2015-03-22)
Dadurch dass die Lösungen durch die Häuser dürfen wird es zum Langweiler
Dadurch dass die Lösungen durch die Häuser dürfen wird es zum Langweiler
piet (2017-03-08)
das wer mal eine aufgabe von Juno oder so. sie geht nicht auf.
das wer mal eine aufgabe von Juno oder so. sie geht nicht auf.
manfred (2017-08-28)
es gibt eine lösung ganz einfach kein mathematik nötig
es gibt eine lösung ganz einfach kein mathematik nötig
Christina (2017-09-05)
Klar geht das..
Vom linken Werk werden z.B. Leitungen von oben gelegt.. und von dem mittleren und rechten gehen die Leitungen mehr oder weniger parallel zu den Häusern ohne sich zu kreuzen.. fertig
Klar geht das..
Vom linken Werk werden z.B. Leitungen von oben gelegt.. und von dem mittleren und rechten gehen die Leitungen mehr oder weniger parallel zu den Häusern ohne sich zu kreuzen.. fertig
Fake News (2017-11-03)
Wow, Leitungen des Nachbarn die durch mein Haus gehen, das würde ich nicht als eine akzeptable Lösung ansehen.
Wow, Leitungen des Nachbarn die durch mein Haus gehen, das würde ich nicht als eine akzeptable Lösung ansehen.
Horst K. (2017-12-19)
Die angegebene Lösung ist falsch!
Die richtige Lösung ist, dass man die letzte Leitung dreidimensional ÜBER die beiden anderen Häuser laufen lässt und dann zu dem Haus führt, dem noch der letzte Anschluss fehlt. Man muss also die zweidimensionale Perspektive verlassen. NUR SO ist dieses Rätsel KORREKT lösbar. Die letzte Leitung geht dabei nicht DURCH, sondern über die beiden anderen Häuser und sie kreuzt keine andere Leitung, wenn man es richtig macht. Somit sind alle Kriterien erfüllt, die zu dieser Aufgabe gehören.
Die angegebene Lösung ist falsch!
Die richtige Lösung ist, dass man die letzte Leitung dreidimensional ÜBER die beiden anderen Häuser laufen lässt und dann zu dem Haus führt, dem noch der letzte Anschluss fehlt. Man muss also die zweidimensionale Perspektive verlassen. NUR SO ist dieses Rätsel KORREKT lösbar. Die letzte Leitung geht dabei nicht DURCH, sondern über die beiden anderen Häuser und sie kreuzt keine andere Leitung, wenn man es richtig macht. Somit sind alle Kriterien erfüllt, die zu dieser Aufgabe gehören.
Stoner (2018-10-17)
Ich habe die Lösung ! Wie bekomm ich hier das Bild hochgeladen
Ich habe die Lösung ! Wie bekomm ich hier das Bild hochgeladen
Ceyda (2019-06-04)
Ne also ich sitze hier seit 2 Stunden und kriege es NICHT hin es giebt keine Lösung alles ist UNNMÖGLICH
Ne also ich sitze hier seit 2 Stunden und kriege es NICHT hin es giebt keine Lösung alles ist UNNMÖGLICH
Herbert J. (2020-10-21)
Habe vor ca. 60 Jahren die Lösung von einem älteren Herrn, einem Tüftler vor dem Herrn, erfahren. Die Lösung ist 100% möglich, auch wenn das keiner glaubt. Hab mir die Lösung leider nicht notiert. Habs immer wieder probiert, kriege es aber nicht mehr hin!
Habe vor ca. 60 Jahren die Lösung von einem älteren Herrn, einem Tüftler vor dem Herrn, erfahren. Die Lösung ist 100% möglich, auch wenn das keiner glaubt. Hab mir die Lösung leider nicht notiert. Habs immer wieder probiert, kriege es aber nicht mehr hin!
Matheverzweifelt (2021-02-24)
Das ist waaaaaaaaaaaaaansig schwer aber jetzt haben ich und meine Mutter das richtige Ergebnis verstanden ich danke dieser SEITE vielen vielen Dank
Das ist waaaaaaaaaaaaaansig schwer aber jetzt haben ich und meine Mutter das richtige Ergebnis verstanden ich danke dieser SEITE vielen vielen Dank
ffzgtr (2021-05-04)
Ich stimme Genieblue zu
Ich stimme Genieblue zu
xxx (2021-08-28)
Ohne zumindest eine Leitung durch ein Haus zu führen gibt es keine Lösung in der Ebene!
Mathematisch handelt es sich dann um einen K3, 3 Graphen und dieser ist nicht planar.
Beweis:
mit 2 Häusern und 2 Kraftwerken ergibt sich folgende triviale Lösung:
H1-------K1
l A1 l A2
K2-------H2
Man sieht, dass sich ein geschlossener Graph ergibt der die Ebene in zwei Flächen teilt.
Wird nun ein Haus (oder Kraftwerk) hinzugefügt, lässt sich dieses wiederum ohne Probleme mit den beiden Kraftwerken (oder Häusern) verbinden. Es wird dadurch aber A1 oder A2 wieder in zwei Flächen geteilt.
Wir haben nun also drei Flächen. Jede dieser Flächen wird von 3 Kanten begrenzt und hat vier Knoten (2 Häuser und 2 Kraftwerke) . Das dritte Kraftwerk (oder Haus) muss nun in einer dieser Flächen liegen und kann somit nur mit den vier Knoten verbunden werden,
Der 5te liegt aber jedenfalls außerhalb der Fläche und kann nicht erreicht werden. qed
Ohne zumindest eine Leitung durch ein Haus zu führen gibt es keine Lösung in der Ebene!
Mathematisch handelt es sich dann um einen K3, 3 Graphen und dieser ist nicht planar.
Beweis:
mit 2 Häusern und 2 Kraftwerken ergibt sich folgende triviale Lösung:
H1-------K1
l A1 l A2
K2-------H2
Man sieht, dass sich ein geschlossener Graph ergibt der die Ebene in zwei Flächen teilt.
Wird nun ein Haus (oder Kraftwerk) hinzugefügt, lässt sich dieses wiederum ohne Probleme mit den beiden Kraftwerken (oder Häusern) verbinden. Es wird dadurch aber A1 oder A2 wieder in zwei Flächen geteilt.
Wir haben nun also drei Flächen. Jede dieser Flächen wird von 3 Kanten begrenzt und hat vier Knoten (2 Häuser und 2 Kraftwerke) . Das dritte Kraftwerk (oder Haus) muss nun in einer dieser Flächen liegen und kann somit nur mit den vier Knoten verbunden werden,
Der 5te liegt aber jedenfalls außerhalb der Fläche und kann nicht erreicht werden. qed
Dan (2022-09-30)
Es gibt für diese Aufgabe keine Lösung. Man bekommt 8 Leitungen gelegt. Mit der 9. kommt man nicht mehr durch da man mit den 8 sämtliche Wege versperrt hat. Egal wie sie gelegt werden.
Es gibt für diese Aufgabe keine Lösung. Man bekommt 8 Leitungen gelegt. Mit der 9. kommt man nicht mehr durch da man mit den 8 sämtliche Wege versperrt hat. Egal wie sie gelegt werden.
Dr. Zweistein (2023-07-23)
Es gibt eine Lösung!!! z.B. Auf der Oberfläche einer Kaffeetasse.
Probiert es aus.
Es gibt eine Lösung!!! z.B. Auf der Oberfläche einer Kaffeetasse.
Probiert es aus.
Hallo (2024-06-17)
Habt jemand ne Lösung?
Habt jemand ne Lösung?
Neuen Kommentar schreiben: